MAPA - GEOMETRIA ANALÍTICA E ÁLGEBRA LINEAR

ETAPA I – TAMANHO DAS CORREIAS
 
Imagine que você é trainee em uma empresa que trabalha com a distribuição de peças mecânicas. Em uma das reuniões de rotina, a gerência apresentou um novo projeto, que corresponde a instalação de novas correias transportadoras em um de seus galpões.
Você foi envolvido no projeto para auxiliar nas estimativas iniciais. Considerando que as correias não possuem elevação, que a Correia I inicia na posição de coordenadas (30,30) e acaba em (40,10), e que a Correia II começa em (40,10) e acaba em (60,40):
a) Qual o tamanho da Correia I?
b) Qual o tamanho da Correia II?
c) Se fosse necessária uma terceira correia (Correia III), ligando o final da correia II ao início da correia I, qual tamanho ela teria?

Observação: As correias devem ter o dobro do tamanho da distância entre seu início e seu fim. O ponto (0,0) corresponde à entrada principal do galpão. As coordenadas estão em metros.

ETAPA II – MATRIZ DAS DEMANDAS

A ideia de instalar essas novas correias motivou novas ações, incluindo a interligação dos diversos galpões da empresa, com o intuito de otimizar o tempo de transporte de itens de um para outro.
A seguir estão apresentados os galpões e quais os fluxos possíveis de transporte de peças mecânicas.
 

Figura 1 - Disposição espacial dos galpões

 

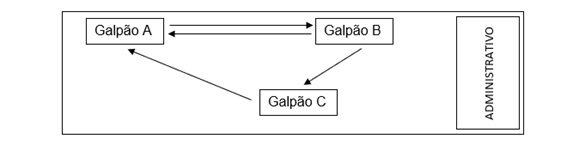
Em situações como essa, podemos usar uma matriz para simular a inter-relação entre os galpões. Seu supervisor gostaria que analisasse os fluxos entre os galpões usando matrizes e como exemplo, ele apresentou a situação a seguir:

Pode-se representar essa situação como uma matriz, em que, na primeira linha apresentam-se as ligações entre A e demais pontos e na segunda linha apresentam-se as ligações entre B e demais pontos. Se há fluxo, o elemento na matriz será “1”, se não houver, o elemento será zero. Sendo assim, como se tem duas posições, deve-se considerar uma matriz 2x2:

Percebe-se que A não se liga com ele mesmo, por isso o elemento da primeira linha/primeira coluna será zero, mas será 1 na segunda coluna, pois há fluxo de A para B. Já posição B não tem fluxo levando a nenhuma posição.
a) Apresente a matriz A, que representa os fluxos de peças entre os galpões.
b) Apresente a matriz D, que representa as quantidades totais das demandas, em milhões de unidades, definida pela matriz A multiplicada pela matriz M.

ETAPA III – OCUPAÇÃO
 
Existe uma maneira de calcular a ocupação de cada galpão, utilizando a matriz D das demandas, que corresponde à resposta da questão “b” da ETAPA II.
Para isso, primeiramente, é preciso calcular os autovalores da matriz D. Depois escolha o autovetor que corresponde ao autovalor mais alto dentre os autovalores calculados. Divida cada coordenada do autovetor pela soma de suas coordenadas. Os valores encontrados vão corresponder à ocupação dos galpões, respectivamente, do Galpão A, do Galpão B e do Galpão C.

a) Calcule os autovalores da matriz D.
b) Apresente o autovalor de valor mais alto.
c) Apresente o autovetor do autovalor calculado em “b”.
d) Calcule as ocupações de cada galpão.

 

MAPA - GEOMETRIA ANALÍTICA E ÁLGEBRA LINEAR  

R$60,00 CHAVE PIX eng.carlosjfilho@hotmail.com

Contatos